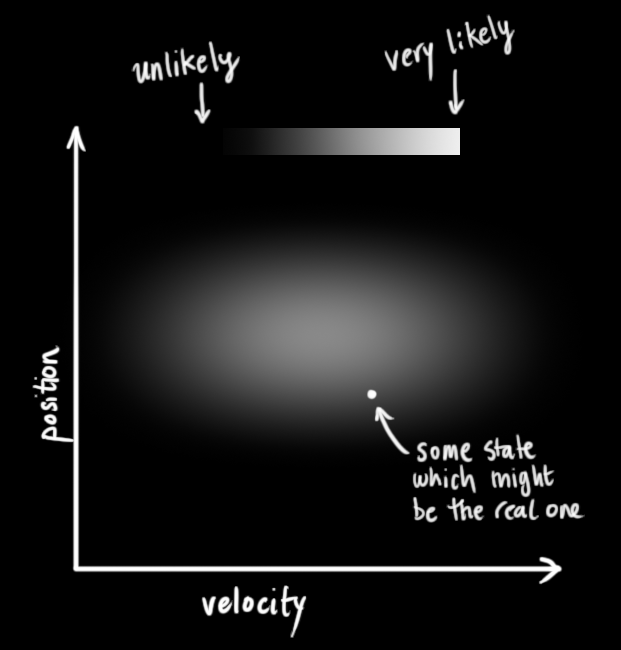
OK, so I was considering what's a Dirichlet distribution and what's a categorical, because I don't know what a slice from the area chart of activities over 24 hours (you know the one) would be. I guess categorical, not Dirichlet, because it's a rigid group of probabilities, like the Bernoulli
Good visualization of Bernoulli: gave me an "aha".
Then onwards to the categorical. Look!
This is a regular Cartesian 3-D coordinate system, so you're meant to see the triangle as standing slanted against the vertical axis. Make sense?
The entire triangle is not a categorical distribution; rather, the triangle is the space of all possible categorical distributions. One distribution would be a single point on it. A tuple of three p-values that add up to 1.
This triangle visualization is important, because now see the Dirichlet:
en.wikipedia.org/wiki/File:Dirichlet.pdf
Now let's backtrack to the Bernoulli and beta distributions to make sure you understand it. Does the beta make sense to you – are you fully clear on what the x and y axes represent?
At any point on the x-axis between 0 and 1, you have a tuple of two values p and (1-p). So, x = 0.3 represents the Bernoulli distribution where p = 0.3 and 1-p = 0.7. And the y-axis says how likely you are to observe this particular tuple. Yes, kind of a "probability of a probability"… Although x could represent any number-pair that has to add to 1 or some other given fixed sum.
But really, when you model a generative process as a Bernoulli of unknown parameters, it makes sense to have, as prior, a probability distribution over all possible Bernoulli distributions, so yes, a prob of a prob.
You might think p = 0.1 and 1-p = 0.9 is a likely description of the generative process behind some variable but the reversed pair is not, so for your beta prior you might set α = 2 and β = 5 (orange line here).
So that one area chart is a distribution of categoricals over time.
A distribution of Dirichlets over time would be like if we took one of those triangles and extrude it out like a Toblerone. If we imagine the white background as invisible, it might look like a blue snake in the midst of writhing around.
This led me to ask what a Dirichlet process is. Ok, first it's a stochastic process. Are they always over time? Of course not necessarily, but what exemplifies it as a process is there's usually some relation to "past" values or simply "neighboring values on one axis", that axis not being one of the parameters to the Dirichlet itself.
A simple stochastic process is the Bernoulli process, which you'll recognize as the coin-flip process. A sequence of iid rv where each rv takes values 0 or 1. There's no autocorrelation of any kind. We can still draw a contiguous line on a chart if we consider each draw of the process as the sum of all previous draws.
A random walk is similar. The simple random walk is like the coin-flip process, but the rv takes values of 1 or -1 instead of 1 or 0. Interestingly, it's kind of hard to define one on continuous time – normally the steps in the time t are discrete.
The Wiener process, historically also called the Brownian motion process, is based on the normal distribution instead of the Bernoulli. The size of each change is distributed per the Gaussian.
Apparently, the Wiener process is a member of several families of processes: Markov processes, Levy processes and Gaussian processes.
The Wiener is Markovian, really? This leads me to: what is a Markov process? Wikipedia and Google seem to treat the term as synonymous with a Markov chain.
Generally, "a Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event."
As with most processes, there is a distinction between discrete-time (DTMC) and continuous time (CTMC) Markov chains.